0/1 Knapsack Problem Memory function.

0/1 Knapsack Problem Memory function

Definition:

Given a set of n items of known weights w1,…,wn and values v1,…,vn and a knapsack of capacity W, the problem is to find the most valuable subset of the items that fit into the knapsack.

Knapsack problem is an OPTIMIZATION PROBLEM

Dynamic programming approach to solve knapsack problem

Step 1:

Identify the smaller sub-problems. If items are labeled 1..n, then a sub-problem would be to find an optimal solution for Sk = {items labeled 1, 2, .. k}

Step 2:

Recursively define the value of an optimal solution in terms of solutions to smaller problems.

Initial conditions:

Step 3:

Bottom up computation using iteration

Question:

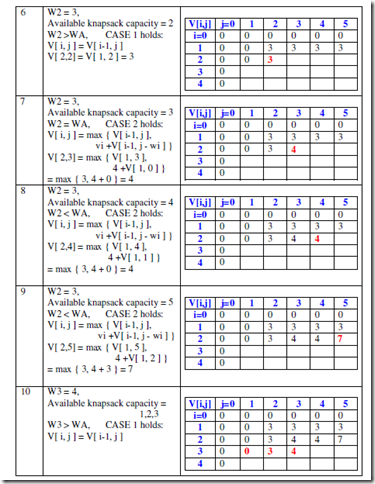
Apply bottom-up dynamic programming algorithm to the following instance of the knapsack problem Capacity W= 5

Solution:

Using dynamic programming approach, we have:

What is the composition of the optimal subset?

The composition of the optimal subset if found by tracing back the computations for the entries in the table.

Efficiency:

• Running time of Knapsack problem using dynamic programming algorithm is:

O( n * W )

• Time needed to find the composition of an optimal solution is: O( n + W )

Memory function

• Memory function combines the strength of top-down and bottom-up approaches

• It solves ONLY sub-problems that are necessary and does it ONLY ONCE.

The method:

• Uses top-down manner.

• Maintains table as in bottom-up approach.

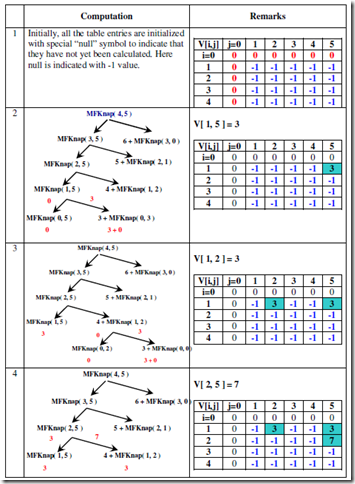
• Initially, all the table entries are initialized with special “null” symbol to indicate that they have not yet been calculated.

• Whenever a new value needs to be calculated, the method checks the corresponding entry in the table first:

• If entry is NOT “null”, it is simply retrieved from the table.

• Otherwise, it is computed by the recursive call whose result is then recorded in the table.

Algorithm:

Example:

Apply memory function method to the following instance of the knapsack problem Capacity W= 5

Solution:

Using memory function approach, we have:

Efficiency:

• Time efficiency same as bottom up algorithm: O( n * W ) + O( n + W )

• Just a constant factor gain by using memory function

• Less space efficient than a space efficient version of a bottom-up algorithm