Greedy technique and spanning tree.

By -

GREEDY TECHNIQUE

Definition:

Greedy technique is a general algorithm design strategy, built on following elements:

• configurations: different choices, values to find

• objective function: some configurations to be either maximized or minimized

The method:

• Applicable to optimization problems ONLY

• Constructs a solution through a sequence of steps

• Each step expands a partially constructed solution so far, until a complete solution to the problem is reached.

On each step, the choice made must be

• Feasible: it has to satisfy the problem’s constraints

• Locally optimal: it has to be the best local choice among all feasible choices available on that step

• Irrevocable: Once made, it cannot be changed on subsequent steps of the algorithm

NOTE:

• Greedy method works best when applied to problems with the greedy-choice property

• A globally-optimal solution can always be found by a series of local improvements from a starting configuration.

Greedy method vs. Dynamic programming method:

• LIKE dynamic programming, greedy method solves optimization problems.

• LIKE dynamic programming, greedy method problems exhibit optimal substructure

• UNLIKE dynamic programming, greedy method problems exhibit the greedy choice property -avoids back-tracing.

Applications of the Greedy Strategy:

• Optimal solutions:

Change making

Minimum Spanning Tree (MST)

Single-source shortest paths

Huffman codes

• Approximations:

Traveling Salesman Problem (TSP)

Fractional Knapsack problem

Spanning Tree

Definition:

Spanning tree is a connected acyclic sub-graph (tree) of the given graph (G) that includes all of G’s vertices

Example: Consider the following graph

image

Minimum Spanning Tree (MST) Definition:

MST of a weighted, connected graph G is defined as: A spanning tree of G with minimum total weight.

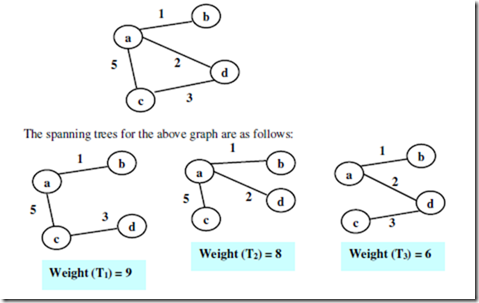
Example: Consider the example of spanning tree:

For the given graph there are three possible spanning trees. Among them the spanning tree with the minimum weight 6 is the MST for the given graph

Question: Why can’t we use BRUTE FORCE method in constructing MST ?

Answer: If we use Brute force method-

• Exhaustive search approach has to be applied.

• Two serious obstacles faced:

1. The number of spanning trees grows exponentially with graph size.

2. Generating all spanning trees for the given graph is not easy.

MST Applications:

• Network design.

Telephone, electrical, hydraulic, TV cable, computer, road

• Approximation algorithms for NP-hard problems.

Traveling salesperson problem, Steiner tree

• Cluster analysis.

• Reducing data storage in sequencing amino acids in a protein

• Learning salient features for real-time face verification

• Auto config protocol for Ethernet bridging to avoid cycles in a network, etc

Comments

Post a Comment

Popular posts from this blog

Data Structure Visualization:Introduction and Value of Data Structure Rendering

By -
Introduction Important advances in programming languages have occurred since the early days of assembly languages and op codes, and modern programming languages have significantly simplified the task of writing computer programs. Unfortunately, tools for un d e rstanding programs have not achieved the accompanying levels of improvement. Software developers still face difficulties in understanding, analyzing, debugging, and improving code. As an example of the difficulties still evident, consider a developer who has just implemented a new algorithm and is now ready to examine the program’s behavior. After issuing a command to begin program execution, the developer examines output data and/or inter- active behavior, attempting to ascertain if the program functioned correctly, and if not, the reasons for the program’s failure. This task can be laborious and usually requires the use of a debugger or perhaps even the addition of explicit checking code, usually through output statements. Furt
Read more

Binary Space Partitioning Trees:BSP Tree as a Hierarchy of Regions.

By -
Image
BSP Tree as a Hierarchy of Regions Another way to look at BSP Trees is to focus on the hierarchy of regions created by the recursive partitioning, instead of focusing on the hyperplanes themselves. This view helps us to see more easily how intersections are efficiently computed. The key idea is to think of a BSP Tree region as serving as a bounding volume: each node v corresponds to a convex volume that completely contains all the geometry represented by the sub tree rooted at v . Therefore, if some other geometric entity, such as a point, ray, object, etc., is found to not intersect the bounding volume, then no intersection computations need be performed with any geometry within that volume. Consider as an example a situation in which we are given some test point and we want to find which object if any this point lies in. Initially, we know only that the point lies somewhere space ( Figure 20.12). By comparing the location of the point with respect to the first partitioning hyper pl
Read more

Drawing Trees:HV-Layout

By -
Image
HV-Layout An hv -layout of a binary tree is an upward (but not strictly upward) straight line orthogonal drawing with edges drawn as rightward horizontal or downward vertical segments. The ”hv” stands for horizontal-vertical. For any vertex v in a binary tree T we either have: 1. A child of v is either • aligned horizontally with v and to the right of v or • vertically aligned below v . 2. The smallest rectangles that cover the area of the subtrees of the children of v in the layout do not intersect. Figure 45.12 shows an example of a hv -layout A hv -layout is generated by applying a dived and conquer approach. The divide step constructs the hv -layout of the left and the right subtrees, while the conquer step either performs a ho rizontal or a ver t i c a l combination . Figure 45.13 shows the two types of com- bination. If the left subtree a node v is placed to the left in a horizontal combination and below in a vertical combination, the layout preserves
Read more