Insertion sort

Insertion sort

Description:

Insertion sort is an application of decrease & conquer technique. It is a comparison based

sort in which the sorted array is built on one entry at a time

Algorithm:

ALGORITHM Insertionsort(A [0 … n-1] )

//sorts a given array by insertion sort

//i/p: Array A[0…n-1]

//o/p: sorted array A[0…n-1] in ascending order

Analysis:

• Input size: Array size, n

• Basic operation: key comparison

• Best, worst, average case exists

Best case: when input is a sorted array in ascending order: Worst case: when input is a sorted array in descending order:

•  Let Cworst(n) be the number of key comparison in the worst case. Then

• Let Cbest(n) be the number of key comparison in the best case.

Then

Example:

Sort the following list of elements using insertion sort:

89, 45, 68, 90, 29, 34, 17

Advantages of insertion sort:

• Simple implementation. There are three variations

o Left to right scan

o Right to left scan

o Binary insertion sort

• Efficient on small list of elements, on almost sorted list

• Running time is linear in best case

• Is a stable algorithm

• Is a in-place algorithm

Depth-first search (DFS) and Breadth-first search (BFS)

DFS and BFS are two graph traversing algorithms and follow decrease and conquer approach – decrease by one variation to traverse the graph

Some useful definition:

• Tree edges: edges used by DFS traversal to reach previously unvisited vertices

• Back edges: edges connecting vertices to previously visited vertices other than their immediate predecessor in the traversals

• Cross edges: edge that connects an unvisited vertex to vertex other than its immediate predecessor. (connects siblings)

• DAG: Directed acyclic graph

Depth-first search (DFS)

Description:

• DFS starts visiting vertices of a graph at an arbitrary vertex by marking it as visited.

• It visits graph’s vertices by always moving away from last visited vertex to an unvisited one, backtracks if no adjacent unvisited vertex is available.

• Is a recursive algorithm, it uses a stack

• A vertex is pushed onto the stack when it’s reached for the first time

• A vertex is popped off the stack when it becomes a dead end, i.e., when there is no adjacent unvisited vertex

• “Redraws” graph in tree-like fashion (with tree edges and back edges for undirected graph)

Algorithm:

ALGORITHM DFS (G)

//implements DFS traversal of a given graph

//i/p: Graph G = { V, E}

//o/p: DFS tree

Mark each vertex in V with 0 as a mark of being “unvisited”

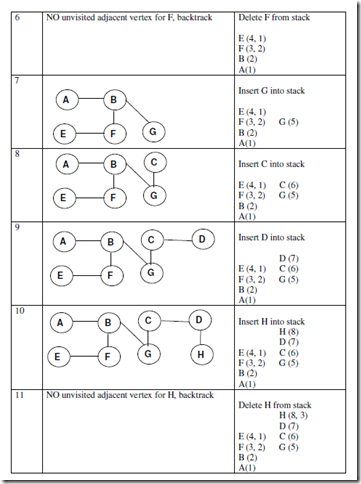
Example:

Starting at vertex A traverse the following graph using DFS traversal method:

The DFS tree is as follows: (dotted lines are back edges)

Applications of DFS:

• The two orderings are advantageous for various applications like topological sorting, etc

• To check connectivity of a graph (number of times stack becomes empty tells the number of components in the graph)

• To check if a graph is acyclic. (no back edges indicates no cycle)

• To find articulation point in a graph

Efficiency:

• Depends on the graph representation:

o Adjacency matrix : Θ(n2)

o Adjacency list: Θ(n + e)

Breadth-first search (BFS)

Description:

• BFS starts visiting vertices of a graph at an arbitrary vertex by marking it as visited.

• It visits graph’s vertices by across to all the neighbors of the last visited vertex

• Instead of a stack, BFS uses a queue

• Similar to level-by-level tree traversal

• “Redraws” graph in tree-like fashion (with tree edges and cross edges for undirected graph)

Algorithm:

Example:

Starting at vertex A traverse the following graph using BFS traversal method:

Applications of BFS:

• To check connectivity of a graph (number of times queue becomes empty tells the number of components in the graph)

• To check if a graph is acyclic. (no cross edges indicates no cycle)

• To find minimum edge path in a graph

Efficiency:

• Depends on the graph representation:

o Array : Θ(n2)

o List: Θ(n + e)

Difference between DFS & BFS: