Floyd’s Algorithm to find -ALL PAIRS SHORTEST PATHS.

Floyd’s Algorithm to find

-ALL PAIRS SHORTEST PATHS

Some useful definitions:

• Weighted Graph: Each edge has a weight (associated numerical value). Edge weights may represent costs, distance/lengths, capacities, etc. depending on the problem.

• Weight matrix: W(i,j) is

o 0 if i=j

o ∞ if no edge b/n i and j.

o “weight of edge” if edge b/n i and j.

Problem statement:

Given a weighted graph G( V, Ew), the all-pairs shortest paths problem is to find the shortest path between every pair of vertices ( vi, vj ) Є V.

Solution:

A number of algorithms are known for solving All pairs shortest path problem

• Matrix multiplication based algorithm

• Dijkstra's algorithm

• Bellman-Ford algorithm

• Floyd's algorithm

Underlying idea of Floyd’s algorithm:

• Let W denote the initial weight matrix.

• Let D(k) [ i, j] denote cost of shortest path from i to j whose intermediate vertices are a subset of {1,2,…,k}.

• Recursive Definition Case 1:

A shortest path from vi to vj restricted to using only vertices from {v1,v2,…,vk} as intermediate vertices does not use vk. Then

D(k) [ i, j ] = D(k-1) [ i, j ].

Case 2:

A shortest path from vi to vj restricted to using only vertices from {v1,v2,…,vk} as intermediate vertices do use vk. Then

D(k) [ i, j ] = D(k-1) [ i, k ] + D(k-1) [ k, j ].

We conclude:

D(k)[ i, j ] = min { D(k-1) [ i, j ], D(k-1) [ i, k ] + D(k-1) [ k, j ] }

Algorithm:

Algorithm Floyd(W[1..n, 1..n])

// Implements Floyd’s algorithm

// Input: Weight matrix W

// Output: Distance matrix of shortest paths’ length

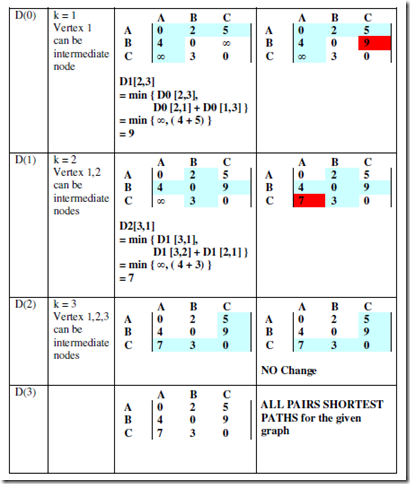
Example:

Find All pairs shortest paths for the given weighted connected graph using Floyd’s algorithm.