Heaps and Heap sort.

By -

Heaps

Definition:

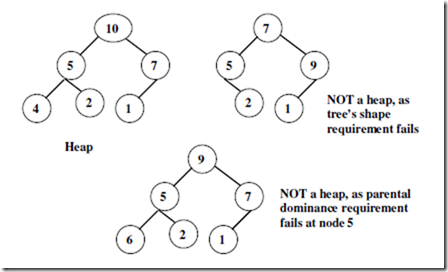
A heap is a binary tree with keys assigned to its nodes, provided the following two conditions are met:

i. Tree’s shape requirement: The binary tree is essentially complete, all its level are full except possibly the last level, where only some rightmost leaves may be missing.

ii. Parental dominance requirement: The key at each node is greater than or equal to the keys at its children.

Example:

image

Important properties of heap

1. There exists exactly one essentially complete binary tree with n nodes. Its height is

equal to └ log2n ┘

2. The root of a heap always contains its largest element

3. A node of a heap considered with all its descendents is also a heap.

4. A heap can be implemented as an array by recording its elements in the top-down, left-to-right fashion. Heap elements are stored in positions 1 through n of an array. In such representation:

a. The parental node keys will be in the first └ n/2 ┘ positions of the array, while the leaf keys will occupy the last ┌n/2┐ positions.

b. The children of a key in the array’s parental position i (1 ≤ i ≤ └ n/2 ┘ ) will be in position 2i and 2i +1, and, correspondingly the parent of a key in position i (2 ≤ i ≤ n) will be in position └ i/2 ┘

Example:

image

Heap construction

Construct heap for the list: 2, 9, 7, 6, 5, 8

There are two methods for heap construction:

1. Top-down construction: Constructs a heap by successive insertions of a new key into a previously constructed heap.

Insert 2 into empty tree

image

image

2. Bottom - up construction:

ALGORITHM HeapBottomUp(H[1…n])

//constructs a heap from the elements of a given array by bottom-up algorithm

//i/p: An array H[1…n] of orderable items

//o/p: A heap H[1…n]

image

1.Initialize the essentially complete binary tree with n nodes by placing keys in the order given and then heapify the tree.

image

image

Inserting a key into heap

Example: Insert a key 10 into the heap (9, 6, 8, 2, 6, 7)

Insert the new key as the last node in the heap, then heapify.

imageDeleting a key from heap

Example: Delete the root’s key from the heap (9, 8, 6, 2, 5, 1)

Solution:

MAXIMUM Key Deletion algorithm

Step 1: Exchange the root’s key with the last key K of the heap.

Step 2: Decrease the heap’s size by 1

Step 3: “Heapify” the smaller tree.

image

Heap sort

Description:

• Invented by J.W.J Williams

• It is a two stage algorithm that works as follows:

o Stage 1: (Heap construction): Construct a heap for a given array

o Stage 2: (maximum deletions): Apply the root-deletion operation n-1 times to the remaining heap

Example:

Sort the following lists by heap sort by using the array representation of heaps.

2, 9, 7, 6, 5, 8

image

Efficiency of heap sort:

Heap sort is an in place algorithm. Time required for heap construction + time required for maximum deletion

= O(n) + O(n log n)

= O(n log n)

Comments

Post a Comment

Popular posts from this blog

Data Structure Visualization:Introduction and Value of Data Structure Rendering

By -
Introduction Important advances in programming languages have occurred since the early days of assembly languages and op codes, and modern programming languages have significantly simplified the task of writing computer programs. Unfortunately, tools for un d e rstanding programs have not achieved the accompanying levels of improvement. Software developers still face difficulties in understanding, analyzing, debugging, and improving code. As an example of the difficulties still evident, consider a developer who has just implemented a new algorithm and is now ready to examine the program’s behavior. After issuing a command to begin program execution, the developer examines output data and/or inter- active behavior, attempting to ascertain if the program functioned correctly, and if not, the reasons for the program’s failure. This task can be laborious and usually requires the use of a debugger or perhaps even the addition of explicit checking code, usually through output statements. Furt
Read more

Binary Space Partitioning Trees:BSP Tree as a Hierarchy of Regions.

By -
Image
BSP Tree as a Hierarchy of Regions Another way to look at BSP Trees is to focus on the hierarchy of regions created by the recursive partitioning, instead of focusing on the hyperplanes themselves. This view helps us to see more easily how intersections are efficiently computed. The key idea is to think of a BSP Tree region as serving as a bounding volume: each node v corresponds to a convex volume that completely contains all the geometry represented by the sub tree rooted at v . Therefore, if some other geometric entity, such as a point, ray, object, etc., is found to not intersect the bounding volume, then no intersection computations need be performed with any geometry within that volume. Consider as an example a situation in which we are given some test point and we want to find which object if any this point lies in. Initially, we know only that the point lies somewhere space ( Figure 20.12). By comparing the location of the point with respect to the first partitioning hyper pl
Read more

Drawing Trees:HV-Layout

By -
Image
HV-Layout An hv -layout of a binary tree is an upward (but not strictly upward) straight line orthogonal drawing with edges drawn as rightward horizontal or downward vertical segments. The ”hv” stands for horizontal-vertical. For any vertex v in a binary tree T we either have: 1. A child of v is either • aligned horizontally with v and to the right of v or • vertically aligned below v . 2. The smallest rectangles that cover the area of the subtrees of the children of v in the layout do not intersect. Figure 45.12 shows an example of a hv -layout A hv -layout is generated by applying a dived and conquer approach. The divide step constructs the hv -layout of the left and the right subtrees, while the conquer step either performs a ho rizontal or a ver t i c a l combination . Figure 45.13 shows the two types of com- bination. If the left subtree a node v is placed to the left in a horizontal combination and below in a vertical combination, the layout preserves
Read more