Balanced search trees .

By -

Balanced search trees

Description:

The disadvantage of a binary search tree is that its height can be as large as N-1, which  means that the time needed to perform insertion and deletion and many other operations can be O(N) in the worst case. Balanced binary search tree is a tree with small height, O(log N). (A binary tree with N node has height at least Θ(log N) )

Example of balanced search trees:

• Instance simplification variety AVL trees, Red-black trees

• Representation change variety: 2-3 trees, 2-3-4 trees, B-trees

AVL trees

Definition:

An AVL tree is a binary search tree in which the balance factor (defined as:

difference between the heights of the node’s left and right sub-trees) of every node is either 0 or +1 or -1.

NOTE:

The height of the empty tree is defined as -1

Basic operations like insertion, deletion, searching key, has efficiency as Θ(log n)

image

AVL tree rotation

If an insertion of a new node makes an AVL tree unbalanced, we transform the tree by a rotation.

Rotation Definition:

A rotation in an AVL tree is a local transformation of its sub-tree rooted at a node whose balance has become either +2 or -2.

NOTE:

If there are several such nodes, we rotate the tree rooted at the unbalanced node that is the closest to the newly inserted leaf

Types of rotations:

There are 4 types of rotations:

1. Single R – rotation

2. Single L – rotation

3. Double LR – rotation

4. Double RL – rotation

Single R – rotation

• Single right rotation

• Rotates the edge connecting the root and its left child in the binary tree

• Example:

image

• Here rotation is performed after a new key is inserted into the left sub-tree of the left child of a tree whose root had the balance of +1 before the insertion

Single L – rotation

• Single left rotation

• Rotates the edge connecting the root and its right child in the binary tree

• Example:

image

• Here rotation is performed after a new key is inserted into the right sub-tree of the right child of a tree whose root had the balance of -1 before the insertion

Double LR – rotation

• Double left-right rotation

• Combination of two rotations

1. perform left rotation of the left sub-tree of root r

2. perform right rotation of the new tree rooted at r

• It is performed after a new key is inserted into the right sub-tree of the left child of a tree whose root had the balance of +1 before the insertion

• Example:

image

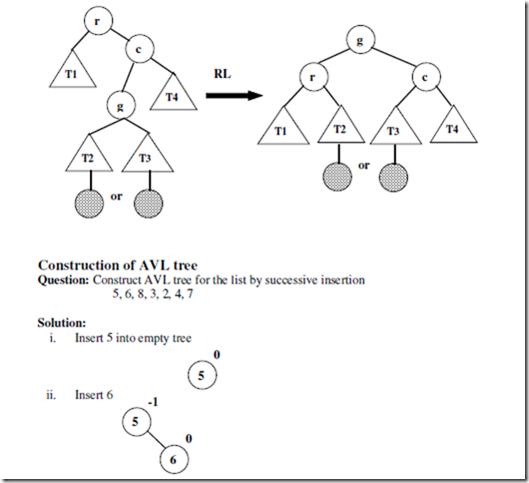
Double RL – rotation

• Double right-left rotation

• Combination of two rotations

1. perform right rotation of the right sub-tree of root r

2. perform left rotation of the new tree rooted at r

• It is performed after a new key is inserted into the left sub-tree of the right child of a tree whose root had the balance of -1 before the insertion

• Example:

image

• General form: A shaded node is the last node inserted. It can be either in the left sub-tree or in the right sub-tree of the root’s grandchild.

image

image

image

Limitations of AVL trees

• Requires frequent rotations to maintain balances for the tree’s nodes

• Even though the deletion operation efficiency is Θ(log n), it is considerably more difficult than insertion

2-3 trees

Definition:

2-3 tree is a height balanced search tree, that has all its leaves on the same level and can

have nodes of two kinds:

• 2-node: contains a single key K and has two children- the left child serves as the root of a sub-tree whose keys are less than K, and the right child serves as the root of a sub-tree whose keys are greater than K

image

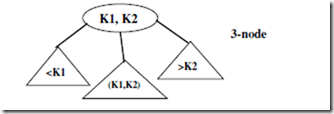
• 3-node: contains two ordered keys K1 and K2, (K1 < K2) and has three children.

The leftmost child serves as the root of a sub-tree with keys less than K1, middle child serves as the root of a sub-tree with keys between K1 and K2, and the rightmost child serves as the root of a sub-tree with keys greater than K2

image

Construction of 2-3 tree:

Question: Construct a 2-3 tree by successive insertion for the following list

9, 5, 8, 3, 2, 4, 7

Solution:

i. Insert 9 into empty tree

image

Comments

Post a Comment

Popular posts from this blog

Data Structure Visualization:Introduction and Value of Data Structure Rendering

By -
Introduction Important advances in programming languages have occurred since the early days of assembly languages and op codes, and modern programming languages have significantly simplified the task of writing computer programs. Unfortunately, tools for un d e rstanding programs have not achieved the accompanying levels of improvement. Software developers still face difficulties in understanding, analyzing, debugging, and improving code. As an example of the difficulties still evident, consider a developer who has just implemented a new algorithm and is now ready to examine the program’s behavior. After issuing a command to begin program execution, the developer examines output data and/or inter- active behavior, attempting to ascertain if the program functioned correctly, and if not, the reasons for the program’s failure. This task can be laborious and usually requires the use of a debugger or perhaps even the addition of explicit checking code, usually through output statements. Furt
Read more

Binary Space Partitioning Trees:BSP Tree as a Hierarchy of Regions.

By -
Image
BSP Tree as a Hierarchy of Regions Another way to look at BSP Trees is to focus on the hierarchy of regions created by the recursive partitioning, instead of focusing on the hyperplanes themselves. This view helps us to see more easily how intersections are efficiently computed. The key idea is to think of a BSP Tree region as serving as a bounding volume: each node v corresponds to a convex volume that completely contains all the geometry represented by the sub tree rooted at v . Therefore, if some other geometric entity, such as a point, ray, object, etc., is found to not intersect the bounding volume, then no intersection computations need be performed with any geometry within that volume. Consider as an example a situation in which we are given some test point and we want to find which object if any this point lies in. Initially, we know only that the point lies somewhere space ( Figure 20.12). By comparing the location of the point with respect to the first partitioning hyper pl
Read more

Drawing Trees:HV-Layout

By -
Image
HV-Layout An hv -layout of a binary tree is an upward (but not strictly upward) straight line orthogonal drawing with edges drawn as rightward horizontal or downward vertical segments. The ”hv” stands for horizontal-vertical. For any vertex v in a binary tree T we either have: 1. A child of v is either • aligned horizontally with v and to the right of v or • vertically aligned below v . 2. The smallest rectangles that cover the area of the subtrees of the children of v in the layout do not intersect. Figure 45.12 shows an example of a hv -layout A hv -layout is generated by applying a dived and conquer approach. The divide step constructs the hv -layout of the left and the right subtrees, while the conquer step either performs a ho rizontal or a ver t i c a l combination . Figure 45.13 shows the two types of com- bination. If the left subtree a node v is placed to the left in a horizontal combination and below in a vertical combination, the layout preserves
Read more