Kinetic Data Structures:A KDS Application Survey
A KDS Application Survey
Even though we have presented kinetic data structures in a geometric setting, there is nothing intrinsically geometric about KDS. The idea of cached assertions that help track an attribute of interest can be applied to many other settings where there is continuous evolution over time punctuated by discrete events, beyond motion in the physical world. For example, consider a graph whose edge weights or capacities are functions of time, as might arise in an evolving communications network. Then the problem of tracking various substructures of interest, such as the minimum spanning tree (MST) of the graph, or a shortest path tree form a source node, can be formulated and studied within the KDS framework.
We present below a quick summary of some of the areas to which kinetic data structures have been applied so far. The are mostly geometric in nature, but several non-geometric examples appear as well.
A number of the original problems for which kinetic data structures were developed are aimed at different measures of how “spread out” a moving set of points in R is—one example is the convex hull, whose maintenance was discussed in the previous subsection.
Other measures of interest include the diameter, width, and smallest area or perimeter bounding rectangle for a moving set S of n points. All these problems can be solved using the kinetic convex hull algorithm above; the efficiency of the algorithms is O(n2+E ), for any E > 0. There are also corresponding Ω(n2) lower bounds for the number of combinatorial changes in these measures. Surprisingly, the best known upper bound for maintaining the smallest enclosing disk containing S is still near-cubic. Extensions of these results to dimensions higher than two are also lacking.
These costs can be dramatically reduced if we consider approximate extent measures. If we are content with (1 + E) approximations to the measures, then an approximate small- est orthogonal rectangle, diameter, and smallest enclosing disk can be maintained with a number of events that is a function E only and not of n [9]. For example, the bound of the number of approximate diameter updates in R under linear motion of the points is O(1/E).
The fundamental proximity structures in computational geometry are the Voronoi Diagram and the Delaunay triangulation (Chapters 62 and 63).
The edges of the Delaunay triangulation contain the closest pair of points, the closest neighbor to each point, as well as a wealth of other proximity information among the points. From the kinetic point of view, these are nice structures, because they admit completely local certifications. Delaunay’s 1934 theorem [22] states that if a local empty sphere condition is valid for each (d−1)- simplex in a triangulation of points in R , then that triangulation must be Delaunay. This makes it simple to maintain a Delaunay triangulation under point motion: an update is necessary only when one of these empty sphere conditions fails. Furthermore, whenever that happens, a local retiling of space (of which the classic “edge-flip” in R2 is a special case) easily restores Delaunayhood. Thus the KDS for Delaunay (and Voronoi) that follows from this theorem is both responsive and efficient—in fact, each KDS event is an external event in which the structure changes. Though no redundant events happen, an exact upper bound for the total number of such events in the worst-case is still elusive even in R2, where the best known upper bound is nearly cubic, while the best lower bound only quadratic [12]. This principle of a set of easily checked local conditions that implies a global property has been used in kinetizing other proximity structures as well. For instance, in the power diagram [14] of a set of disjoint balls, the two closest balls must be neighbors [31]—and this diagram can be kinetized by a similar approach. Voronoi diagrams of more general objects, such as convex polytopes, have also been investigated. For example, in R2 [29] shows how to maintain a compact Voronoi-like diagram among moving disjoint convex polygons; again, a set of local conditions is derived which implies the global correctness of this diagram. As the polygons move, the structure of this diagram allows one to know the nearest pair of polygons at all times.
In many applications the exact L2-distance between objects is not needed and more relaxed notions of proximity suffice. Polyhedral metrics (such as L1 or L∞) are widely used, and the normal unit ball in L2 can be approximated arbitrarily closely by polyhedral approximants. It is more surprising, however, that if we partition the space around each point into a set of polyhedral cones and maintain a number of directional nearest neighbors to each point in each cone, then we can still capture the globally closest pair of points in the L2 metric. By directional neighbors here we mean that we measure distance only along a given direction in that cone. This geometric fact follows from a packing argument and is exploited in [17] to give a different method for maintaining the closest pair of points in d. The advantage of this method is that the kinetic events are changes of the sorted order of the points along a set of directions fixed a priori, and therefore the total number of events is provably quadratic.
Many areas in scientific computation and physical modeling require the maintenance of a triangulation (or more generally a simplicial complex) that approximates a manifold un- dergoing deformation. The problem of maintaining the Delaunay triangulation of moving points in the plane mentioned above is a special case. More generally, local re-triangulations are necessitated by collapsing triangles, and sometimes required in order to avoid undesir- ably “thin” triangles. In certain cases the number of nodes (points) may also have to change in order to stay sufficiently faithful to the underlying physical process; see, for example, [18]. Because in general a triangulation meeting certain criteria is not unique or canonical, it be- comes more difficult to assess the efficiency of kinetic algorithms for solving such problems. The lower-bound results in [4] indicate that one cannot hope for a subquadratic bound on the number of events in the worst case in the maintenance an any triangulation, even if a linear number of additional Steiner points is allowed.
There is large gap between the desired quadratic upper bound and the current state of art. Even for maintaining an arbitrary triangulation of a set of n points moving linearly in the plane, the best-known algorithm processes O(n7/3) events [5] in the worst case. The algorithm actually maintains a pseudotriangulation of the convex hull of the point set and then a triangulation of each pseudotriangle. Although there are only O(n2) events in the pseudotriangulation, some of the events change too many triangles because of high-degree vertices. Unless additional Steiner points are allowed, there are point configurations for which high-degree vertices are inevitable and therefore some of the events will be expensive. A more clever, global argument is needed to prove a near-quadratic upper bound on the total number of events in the above algorithm. Methods that choose to add additional points, on the other hand, have the burden of defining appropriate trajectories for these Steiner points as well. Finally, today no triangulation that guarantees certain quality on the shapes of triangles as well as a subcubic bound on the number of retiling events is known.
Collision Detection
Kinetic methods are naturally applicable to the problem of collision detection between moving geometric objects. Typically collisions occur at irregular intervals, so that fixed- time stepping methods have difficulty selecting an appropriate sampling rate to fit both the numerical requirements of the integrator as well as those of collision detection. A kinetic method based on the discrete events that are the failures of relevant geometric conditions can avoid the pitfalls of both oversampling and undersampling the system. For two moving convex polygons in the plane, a kinetic algorithm where the number of events is a function of the relative separation of the two polygons is given in [23]. The algorithm is based on constructing certain outer hierarchies on the two polygons. Analogous methods for 3D polytopes were presented in [30], together with implementation data.
FIGURE 23.7: Snapshots of the mixed pseudotriangulation of [5]. As the center trapezoid- like polygon moves to the right, the edges corresponding to the next about-to-fail certificate are highlighted.
A tiling of the free space around objects can serve as a proof of non-intersection of the objects. If such a tiling can be efficiently maintained under object motion, then it can be the basis of a kinetic algorithm for collision detection. Several papers have developed techniques along these lines, including the case of two moving simple polygons in the plane [15], or multiple moving polygons [5, 38]. These developments all exploit deformable pseudotri angulations of the free space—tilings which undergo fewer combinatorial changes than, for example, triangulations. An example from [5] is shown in Figure 23.7. The figure shows how the pseudotriangulation adjusts by local retiling to the motion of the inner quadrilateral. The approach of [5] maintains a canonical pseudotriangulation, while others are based on letting a pseudotriangulation evolve according to the history of the motion. It is unclear at this point which is best. An advantage of all these methods is that the number of certificates needed is close to size of the min-link separating subdivision of the objects, and thus sensitive to how intertwined the objects are.
Deformable objects are more challenging to handle. Classical methods, such as bounding volume hierarchies [27], become expensive, as the fixed object hierarchies have to be rebuilt frequently. One possibility for mitigating this cost is to let the hierarchies themselves deform continuously, by having the bounding volumes defined implicitly in terms of object features. Such an approach was developed for flexible linear objects (such as rope or macromolecules), using combinatorially defined sphere hierarchies in [28]. In that work a bounding sphere is defined not in the usual way, via its center and radius, but in an implicit combinatorial way, in terms of four feature points of the enclosed object geometry. As the object deforms these implicitly defined spheres automatically track their assigned features, and therefore the deformation. Of course the validity of the hierarchy has to be checked at each time step and repaired if necessary. What helps here is that the implicitly defined spheres change their combinatorial description rather infrequently, even under extreme deformation. An example is shown in Figure 23.8 where the rod shown is bent substantially, yet only the top-level sphere needs to update its description.
FIGURE 23.8: A thin rod bending from a straight configuration, and a portion of its associated bounding sphere hierarchy. The combinatorially defined sphere hierarchy is stable under deformation. Only the top level sphere differs between the two conformations.
The pseudotriangulation-based methods above can also be adapted to deal with object deformation.
Connectivity and Clustering
Closely related to proximity problems is the issue of maintaining structures encoding connectivity among moving geometric objects. Connectivity problems arise frequently in ad hoc mobile communication and sensor networks, where the viability of links may depend on proximity or direct line-of-sight visibility among the stations desiring to communicate. With some assumptions, the communication range of each station can be modeled by a geometric region, so that two stations can establish a link if and only if their respective regions overlap. There has been work on kinetically maintaining the connected components of the union of a set of moving geometric regions for the case of rectangles [36] and unit disks [33].
Clustering mobile nodes is an essential step in many algorithms for establishing communication hierarchies, or otherwise structuring ad hoc networks. Nodes in close proximity can communicate directly, using simpler protocols; correspondingly, well-separated clusters can reuse scarce resources, such the same frequency or time-division multiplexing communication scheme, without interference. Maintaining clusters of mobile nodes requires a tradeoff between the tightness, or optimality of the clustering, and its stability under motion. In [26] a randomized clustering scheme is discussed based on an iterated leader-election algorithm that produces a number of clusters within a constant factor of the optimum, and in which the number of cluster changes is also asymptotically optimal. This scheme was used in [25] to maintain a routing graph on mobile nodes that is always sparse and in which communication paths exist that are nearly as good as those in the full communication graph.
Another fundamental kinetic question is the maintenance of a minimum spanning tree (MST) among n mobile points in the plane, closely related to earlier work on parametric spanning trees [24] in a graph whose edge weights are functions of a parameter λ (λ is time in the kinetic setting). Since the MST is determined by the sorted order of the edge weights in the graph, a simple algorithm can be obtained by maintaining the sorted list of weights and some auxiliary data structures (such an algorithm is quadratic in the graph size, or O(n4) in our case). This was improved when the weights are linear functions of time to nearly O(n11/6) (subquadratic) for planar graphs or other minor-closed families [6]. When the weights are the Euclidean distances between moving points, only approximation algorithms are known and the best event bounds are nearly cubic [17]. For many other optimization problems on geometric graphs, such as shortest paths for example, the corresponding kinetic questions are wide open.
The problem of maintaining the visible parts of the environment when an observer is moving is one of the classic questions in computer graphics and has motivated significant developments, such as binary space partition trees, the hardware depth buffer, etc. The difficulty of the question increases significantly when the environment itself includes moving objects; whatever visibility structures accelerate occlusion culling for the moving observer, must now themselves be maintained under object motion.
Binary space partitions (BSP) are hierarchical partitions of space into convex tiles obtained by performing planar cuts (Chapter 20).
Tiles are refined by further cuts until the interior of each tile is free of objects or contains geometry of limited complexity. Once a BSP tree is available, a correct visibility ordering for all geometry fragments in the tiles can be easily determined and incrementally maintained as the observer moves. A kinetic algorithm for visibility can be devised by maintaining a BSP tree as the objects move. The key insight is to certify the correctness of the BSP tree through certain combinatorial conditions, whose failure triggers localized tree rearrangements — most of the classical BSP construction algorithms do not have this property. In 2, a randomized algorithm for maintaining a BSP of moving disjoint line segments is given in [11]. The algorithm processes O(n2) events, the expected cost per tree update is O(log n), and the expected tree size is O(n log n). The maintenance cost increases to O(nλs+2(n) log2 n) [7] for disjoint moving triangles in R (s is a constant depending on the triangle motion). Both of these algorithms are based on variants on vertical decompositions (many of the cuts are parallel to a given direction). It turns out that in practice these generate “sliver-like” BSP tiles that lead to robustness issues [19].
As the pioneering work on the visibility complex has shown [40], another structure that is well suited to visibility queries in R is an appropriate pseudotriangulation. Given a moving observer and convex moving obstacles, a full radial decomposition of the free space around the observer is quite expensive to maintain. One can build pseudotriangulations of the free space that become more and more like the radial decomposition as we get closer to the observer. Thus one can have a structure that compactly encodes the changing visibility polygon around the observer, while being quite stable in regions of the free space well occluded from the observer [39].
Result Summary
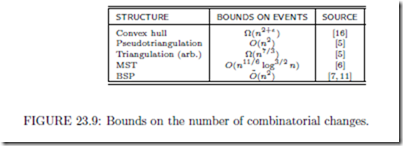
We summarize in Table 23.9 the efficiency bounds on the main KDSs discussed above.
As mentioned above, we still lack efficient kinetic data structures for many fundamental geometric questions. Here is a short list of such open problems:
1. Find an efficient (and responsive, local, and compact) KDS for maintaining the convex hull of points moving in dimensions d ≥ 3.
2. Find an efficient KDS for maintaining the smallest enclosing disk in d ≥ 2. For d = 2, a goal would be an O(n2+E) algorithm.
3. Establish tighter bounds on the number of Voronoi diagram events, narrowing the gap between quadratic and near-cubic.
4. Obtain a near-quadratic bound on the number of events maintaining an arbitrary triangulation of linearly moving points.∗
5. Maintain a kinetic triangulation with a guarantee on the shape of the triangles, in subcubic time.
6. Find a KDS to maintain the MST of moving points under the Euclidean metric achieving subquadratic bounds.
Beyond specific problems, there are also several important structural issues that require further research in the KDS framework. These include:
Recovery after multiple certificate failures.
We have assumed up to now that the KDS assertion cache is repaired after each certificate failure. In many realistic scenarios, however, it is impossible to predict exactly when certificates will fail because explicit motion descriptions may not be available. In such settings we may need to sample the system and thus we must be prepared to deal with multiple (but hopefully few) certificate failures at each time step. A general area of research that this suggests is the study of how to efficiently update common geometric structures, such as convex hulls, Voronoi and Delaunay diagrams, arrangements, etc., after “small motions” of the defining geometric objects.
There is also a related subtlety in the way that a KDS assertion cache can certify the value, or a computation yielding the value, of the attribute of interest. Suppose our goal is to certify that a set of moving points in the plane, in a given circular order, always form a convex polygon. A plausible certificate set for convexity is that all interior angles of the polygon are convex.
See Figure 23.10.
In the normal KDS setting where we can always predict accurately the next certificate failure, it turns out that the above certificate set is sufficient, as long as at the beginning of the motion the polygon was convex. One can draw, however, nonconvex self-intersecting polygons all of whose interior angles are convex, as also shown in the same figure. The point here is that a standard KDS can offer a historical proof of the convexity of the polygon by relying on the fact that the certificate set is valid and that the polygon was convex during the prior history of the motion. Indeed the counterexample shown cannot arise under continuous motion without one of the angle certificates failing first. On the other hand, if an oracle can move the points when “we are not looking,” we can wake up and find all the angle certificates to be valid, yet our polygon need not be convex. Thus in this oracle setting, since we cannot be sure that no certificates failed during the time step, we must insist on absolute proofs — certificate sets that in any state of the world fully validate the attribute computation or value.
Hierarchical motion descriptions.
Objects in the world are often organized into groups and hierarchies and the motions of objects in the same group are highly correlated. For example, though not all points in an elastic bouncing ball follow exactly the same rigid motion, the trajectories of nearby points are very similar and the overall motion is best described as the superposition of a global rigid motion with a small local deformation. Similarly, the motion of an articulated figure, such as a man walking, is most succinctly described as a set of relative motions, say that of the upper right arm relative to the torso, rather than by giving the trajectory of each body part in world coordinates.
What both of these examples suggest is that there can be economies in motion description, if the motion of objects in the environment can be described as a superposition of terms, some of which can be shared among several objects. Such hierarchical motion descrip- tions can simplify certificate evaluations, as certificates are often local assertions concerning nearby objects, and nearby objects tend to share motion components. For example, in a simple articulated figure, we may wish to assert ccw(A, B, C) to indicate that an arm is not fully extended, where AB and BC are the upper and lower parts of the arm respectively. Evaluating this certificate is clearly better done in the local coordinate frame of the upper arm than in a world frame—the redundant motions of the legs and torso have already been factored out.
Motion sensitivity.
As already mentioned, the motions of objects in the world are often highly correlated and it behooves us to find representations and data structures that exploit such motion coherence. It is also important to find mathematical measures that capture the degree of coherence of a motion and then use this as a parameter to quantify the performance of motion algorithms. If we do not do this, our algorithm design may be aimed at unrealistic worst-case behavior, without capturing solutions that exploit the special structure of the motion data that actually arise in practice — as already discussed in a related setting in [20]. Thus it is important to develop a class of kinetic motion-sensitive algorithms, whose performance can be expressed a function of how coherent the motions of the underlying objects are.
Non-canonical structures.
The complexity measures for KDSs mentioned earlier are more suitable for maintaining canonical geometric structures, which are uniquely defined by the position of the data, e.g., convex hull, closest pair, and Delaunay triangulation. In these cases the notion of external events is well defined and is independent of the algorithm used to maintain the structure. On the other hand, as we already discussed, suppose we want to maintain a triangulation of a moving point set. Since the triangulation of a point set is not unique, the external events depend on the triangulation being maintained, and thus depend on the algorithm. This makes it difficult to analyze the efficiency of a kinetic triangulation algorithm. Most of the current approaches for maintaining noncanonical structures artificially impose canonicality and maintain the resulting canonical structure. But this typically increases the number of events. So it is entirely possible that methods in which the current form of the structure may depend on its past history can be more efficient. Unfortunately, we lack mathematical techniques for analyzing such history-dependent structures.






Comments
Post a Comment