String Searching:Introduction and Preliminaries

Introduction

Searching for occurrences of a substring in a text is a common operation familiar to anyone who uses a text editor, word processor, or web browser. It is also the case that algorithms for analyzing textual databases can generate a large number of searches. If a text, such as a portion of the genome of an organism, is to be searched repeatedly, it is sometimes the case that it pays to preprocess the text to create a data structure that facilitates the searches. The suffix tree [5] and suffix array [4] discussed in Chapter 29 are examples.

In this chapter, we give some alternatives to these data structures that have advantages over them in some circumstances, depending on what type of searches or analysis of the text are desired, the amount of memory available, and the amount of effort to be invested in an implementation.

In particular, we focus on the problem of finding the locations of all occurrences of a string x in a text t, where the letters of t are drawn from a fixed alphabet Σ, such as the ASCII letter codes.

The length of a string x, denoted |x|, is the number of characters in it. The empty string, denoted λ is the string of length 0 that has no characters in it. If t = a1a2, ..., an is a text and p = aiai+1...aj is a substring of it, then i is a starting position of p in t, and j is an ending position of p in t. For instance, the starting positions of abc in aabcabcaac are {2, 5}, and its ending positions are {5, 8}. We consider the empty string to have starting and ending positions at {0, 1, 2, ..., n}, once at each position in the text, and once at position 0, preceding the first character of the text. Let EndP ositions(p, t) denote the ending positions of p in t; when t is understood, we may denote it EndP ositions(p).

A deterministic finite automaton on Σ is a directed graph where each directed edge is labeled with a letter from Σ, and where, for each node, there is at most one edge directed out of the node that is labeled with any given letter. Exactly one of the nodes is designated as a start node, and some of the nodes are designated as accept nodes. The label of a directed path is the word given by the sequence of letters on the path. A deterministic finite automaton is used for representing a set of words, namely, the set of the set of labels of paths from the start node to an accept node.

The first data structure that we examine is the directed acyclic word graph. The DAWG is just the deterministic finite automaton representing the set of subwords of a text t. All of its states except for one are accept states. There is no edge from the non-accepting state to any accepting state, so it is convenient to omit the non-accept state when representing the DAWG. In this representation, a string p is a substring of t iff it is the label of a directed path originating at the start node.

There exists a labeling of each node of the DAWG with a set of positions so that the DAWG has the following property:

• Whenever p is a substring of t, its ending positions in t are given by the label of the last node of the path of label p that originates at the start node.

To find the locations where p occurs, one need only begin at the start node, follow edges that match the letters of p in order, and retrieve the set of positions at the node where this process halts.

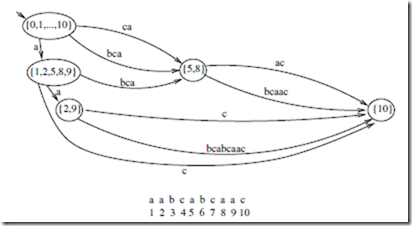
FIGURE 30.1: The DAWG of the text aabcabcaac. The starting node is at the upper left. A string p is a substring of the text if and only if it is the label of a path originating at the start node. The nodes can be labeled so that whenever p is the label of such a path, the last node of the path gives EndP ositions(p). For instance, the strings that lead to the state labeled {5, 8} are ca, bca, and abca, and these have occurrences in the text with their last letter at positions 5 and 8.

In view of the fact that there are Θ(|t|2) intervals on t, each of which represents a substring that is contained in the interval, it is surprising that the number of nodes and edges of the DAWG of t is O(|t|). The reason for this is that all possible query strings fall naturally into equivalence classes, which are sets of strings such that two strings are in the same set if they have the same set of ending positions. The size of an equivalence class can be large, and this economy makes the O(|t|) bound possible.

In an application such as a search engine, one may be interested not in the locations of a string in a text, but the number of occurrences of a string in the text. This is one criterion for deciding which texts are most relevant to a query. Since all strings in an equivalence class have the same number of occurrences, each state can be labeled not with the position set, but with the cardinality of its position set. The label of the node reached on the path labeled p originating at the start node tells the number of occurrences of p in t in O(|p|) time. This variant require O(|t|) space and can be constructed in O(|t|) time.

Unfortunately, the sum of cardinalities of the position sets of the nodes of the DAWG of t is not O(|t|). However, a second data structure that we describe, called the compact DAWG does use O(|t|) space. If a string p has k occurrences in t, then it takes O(|p| + k) time to return the set of occurrences where p occurs in t, given the compact DAWG of t. It can be built in O(|t|) time. These bounds are the same as that for the suffix tree and suffix array, but the compact DAWG requires substantially less space in most cases. An example is illustrated in Figure 30.2.

FIGURE 30.2: The compact DAWG of the text aabcabcaac.

(Compare to Figure 30.1.) The labels depicted in the nodes are the ending positions of the corresponding principal nodes of the DAWG. The compact DAWG is obtained from the DAWG by deleting nodes that have only one outgoing edge, and representing deleted paths between the remaining nodes with edges that are labeled with the path’s label.

Another important issue is the ease with which a programmer can understand and pro- gram the construction algorithm. Like the computer time required for queries, the time spent by a programmer understanding, writing, and maintaining a program is also a re- source that must be considered. The third data structure that we present, called the position heap, has worse worst-case bounds for construction and queries, but has the ad- vantage of being as easy to understand and construct as elementary data structures such as unbalanced binary search trees and heaps. One tradeoff is that the worst-case bounds for a query is O(|p|2 + k), rather than O(|p| + k). However, on randomly generated strings, the expected time for a query is O(|p| + k), and on most practical applications, the query time can be expected not to differ greatly from this. Like the other structures, it can be  constructed in linear time. However, an extremely simple implementation takes O(|t| log |t|) expected time on randomly generate strings, and does not depart much from this in most practical applications. Those who wish to expend minimal programming effort may wish to consider this simple variant of the construction algorithm.

The position heap for the string of Figure 30.1 is illustrated in Figure 30.3.

Preliminaries

The infinite set of all strings that can be formed from letters of an alphabet Σ is denoted Σ∗. If a ∈ Σ, let an denote the string that consists of n repetitions of a.

If x is a string, then for 1 ≤ j ≤ |x|, let xj denote the character in position j. Thus, x can be written as x1x2, ..., x|x|. The reversal x denote the substring xixi+1 , ..., xj .

of x is the string x|x|x|x|−1...x1. Let x[i : j] The prefixes of a string x = x1x2, ..., xk are those with a starting position at the leftmost position of x, namely, the empty string and those strings of the form x[1 : j] for 1 ≤ j ≤ k.

Its suffixes are those with an ending position at the rightmost position of x, namely, the empty string and those of the form x[j : k].

A trie on Σ is a deterministic finite automaton that is a rooted tree whose start node is the root.

Given a family F of subsets of a domain V, the transitive reduction of the subset relation can be viewed as a pointer from each X ∈ F to each Y ∈ F such that X ⊂ Y and there exists no Z such that X ⊂ Z ⊂ Y . This is sometimes referred to as the Hasse diagram of the subset relation on the family. The Hasse diagram is a tree if V ∈ F , ∅ /∈ F , and for each X, Y ∈ F , either X ⊆ Y , Y ⊂ X, or X ∩ Y = ∅.