Drawing Graphs:Convex Drawing
Convex Drawing
A straight-line drawing of a planar graph is convex if all every face is drawn as convex polygon. This section reviews three different algorithms for constructing such a drawing for planar graphs.
Tutte showed that a convex drawing exist for triconnected planar graphs and gave an algorithm for constructing such representations [36, 37].
The algorithm divides the vertex set V into two subsets; a set of fixed vertices and a set of free vertices. The fixed vertices are placed at the vertices of a strictly convex polygon. The positions of free vertices are decided by solving a system of O(n) linear equations, where n is the number of vertices of the graph [37]. In fact, solving the equations is equivalent to placing each free vertex at the barycenter of its neighbors. That is, each position p(v) = (x(v), y(v)) of a vertex v is:
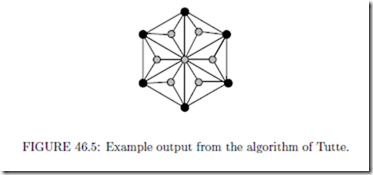
An example of a drawing computed by the barycenter algorithm is illustrated in Figure 46.5. Here the black vertices represent fixed vertices.
The main theorem can be described as follows.
THEOREM 46.1 (Tutte [36, 37]) Suppose that f is a face in a planar embedding of a triconnected planar graph G, and P is a strictly convex planar drawing of f . Then the barycenter algorithm with the vertices of f fixed and positioned according to P gives a convex planar drawing of G.
The matrix resulting from the equations can be solved in O(n1.5) time at best, using a sophisticated sparse matrix elimination method [25]. However, in practice a Newton- Raphson iteration of the equation above converges rapidly.
Divide and Conquer Algorithm
Chiba, Yamanouchi and Nishizeki [6] present a linear time algorithm for constructing convex drawings of planar graphs, using divide and conquer. The algorithm constructs a convex drawing of a planar graph, if it is possible, with a given outside face. The drawing algorithm is based on a classical result by Thomassen [35].
The input to their algorithm is a biconnected plane graph with given outside face and a convex polygon. The output of their algorithm is a convex drawing of the biconnected plane graph with outside face drawn as the input convex polygon, if this is possible. The conditions under which such a drawing is possible come from the following theorem [35].
THEOREM 46.2 (Thomassen [35]) Let G be a biconnected plane graph with outside facial cycle S, and let S∗ be a drawing of S as a convex polygon. Let P1, P2,..., Pk be the paths in S, each corresponding to a side of S∗. (Thus S∗ is a k-gon. It should be noted that not every vertex of the cycle S is necessarily an apex of the polygon S∗.) Then S∗ can be extended to a convex drawing of G if and only if the following three conditions hold.
1. For each vertex v of G − V (S) having degree at least three in G, there are three paths disjoint except at v, each joining v and a vertex of S;
2. The graph G − V (S) has no connected component C such that all the vertices on
S adjacent to vertices in C lie on a single path Pi; and no two vertices in each Pi are joined by an edge not in S; and
3. Any cycle of G which has no edge in common with S has at least three vertices of degree at least 3 in G.
The basic idea of the algorithm of Chiba et al. [6] is to reduce the convex drawing of G to those of several subgraphs of G as follows:
Algorithm ConvexDraw(G, S, S∗)
1. Delete from G an arbitrary apex v of S∗ together with edges incident to v.
2. Divide the resulting graph Gl = G−v into the biconnected components B1, B2,..., Bp.
3.Determine a convex polygon S∗ for the outside facial cycle Si of each Bi so that Bi with S∗ satisfies the conditions in Theorem 46.2.
4.Recursively apply the algorithm to each Bi with S∗ to determine the positions of vertices not in Si.
The main idea of the algorithm is illustrated in Figure 46.6; for more details see [6].
It is easy to show that the algorithm runs in linear time, and its correctness can be established using Theorem 46.2.
THEOREM 46.3 (Chiba, Yamanouchi and Nishizeki [6]) Algorithm Convex Draw constructs a convex planar drawing of a biconnected plane graph with given outside face in linear time, if such a drawing is possible.
Algorithm Using Canonical Ordering
Both the Tutte algorithm and the algorithm of Chiba et al. give poor resolution. Kant [21] gives a linear time algorithm for constructing a planar convex grid drawing of a triconnected
planar graph on a (2n − 4) × (n − 2) grid, where n is the number of vertices. This guarantees that the vertex resolution of the drawing is Ω(1/n).
Kant’s algorithm is based on a method of de Fraysseix, Pach and Pollack [10] for drawing planar triangulated graphs on a grid of size (2n − 4) × (n − 2).
The algorithm of de Fraysseix et al. [10] computes a special ordering of vertices called the canonical ordering based on fixed embedding. Then the vertices are added, one by one, in order to construct a straight-line drawing combined with shifting method. Note that the outside face of the drawing is always triangle, as shown in Figure 46.7.
Kant [21] uses a generalization of the canonical ordering called leftmost canonical ordering. The main difference from the algorithm of de Fraysseix et al. [10] is that it gives a convex drawing of triconnected planar graph. The following Theorem summarizes his main result.
THEOREM 46.4 (Kant [21]) There is a linear time algorithm to construct a planar straight-line convex drawing of a triconnected planar graph with n vertices on a (2n − 4) × (n − 2) grid.
Details of Kant’s algorithm are in [21]. Chrobak and Kant improved the algorithm so that the size of the grid is (n − 2) × (n − 2) [7].






Comments
Post a Comment